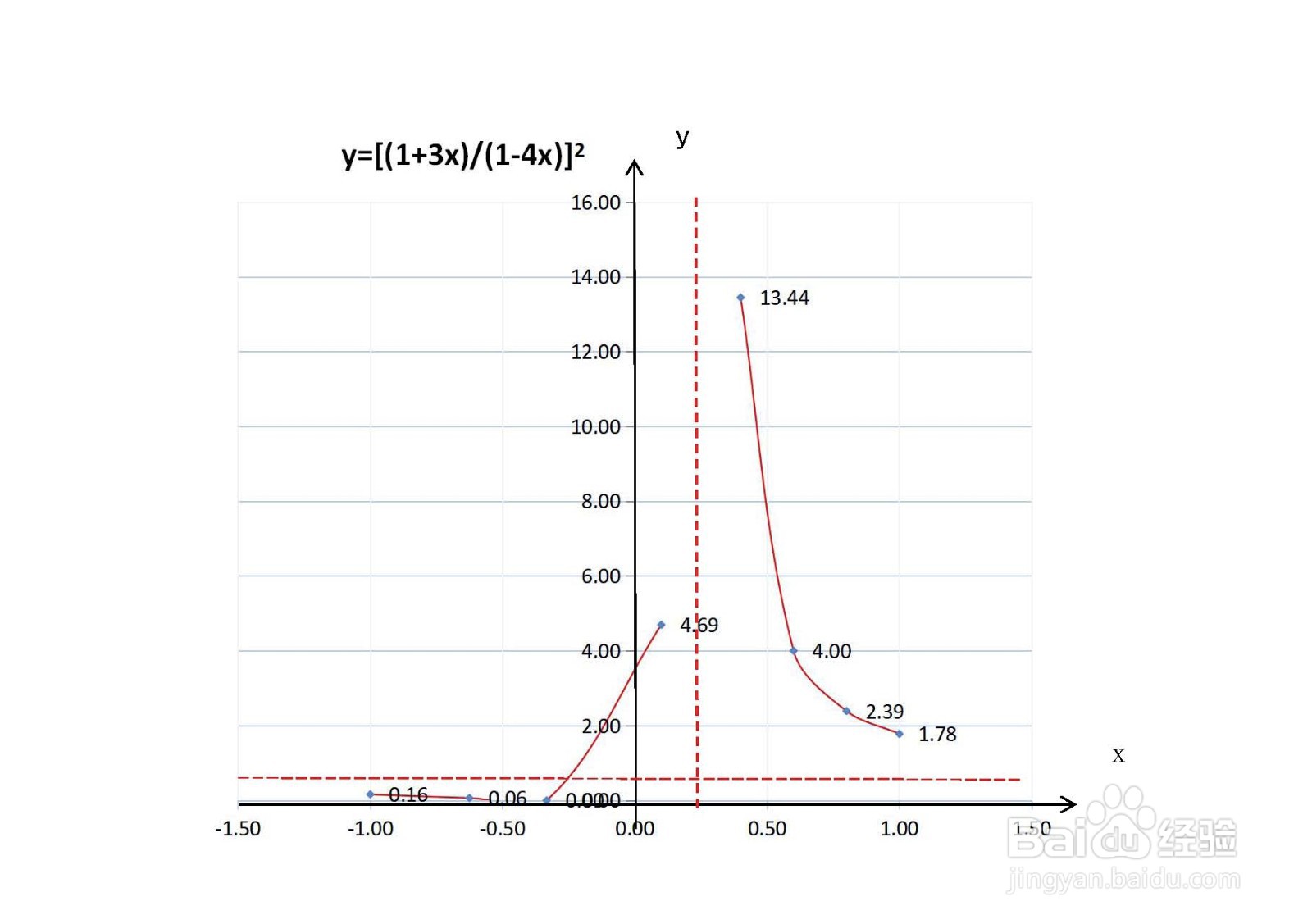
分式复合函数y=(1+3x.1-4x)^2的图像示意图
1、分式函数[(1+3x)/(1-4x)]^2分母不为0,结合分式函数的性质,由分母不为0,求解函数[(1+3x)/(1-4x)]^2的定义域。
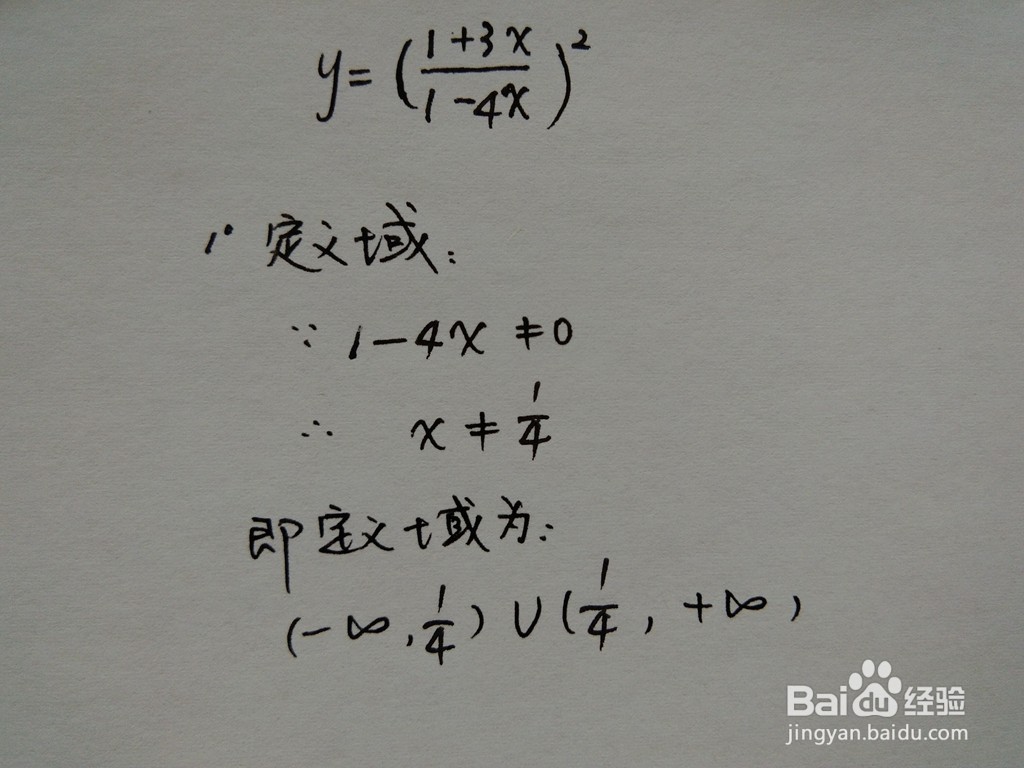
2、函数的单调性也叫函数的增减性。当函数 f(x) 的自变量在其定义区间内增大(或减小)时,函数值f(x)也随着增大(或减小),则称该函数为在该区间上具有单调性。
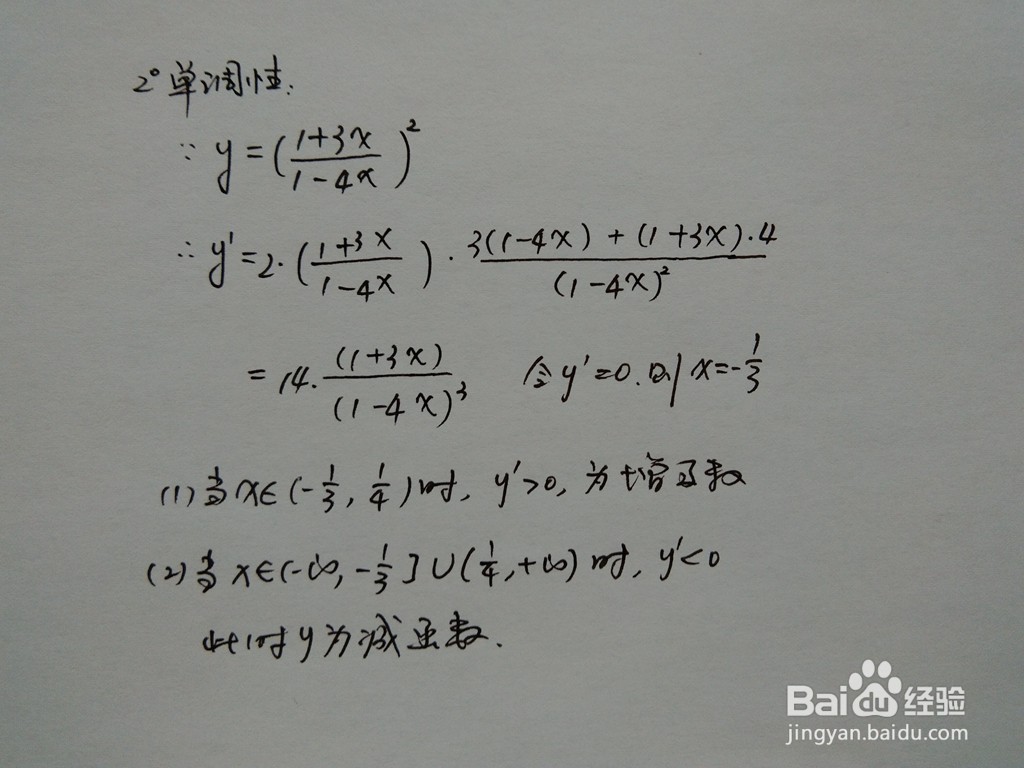
3、根据函数[(1+3x)/(1-4x)]^2求导法则,计算函数的二阶导数,判断函数[(1+3x)/(1-4x)]^2的凸凹性并得到凸凹区间。

4、二阶导数,是原函数导数的导数,将原函数进行二次求导。一般的,函数y=f(x)的导数y'=f'(x)仍然是x的函数,则y'=f'(x)的导数叫作函数y=f(x)的二阶导数。
5、根据题意,解析函数[(1+3x)/(1-4x)]^2在无穷大处的极限。

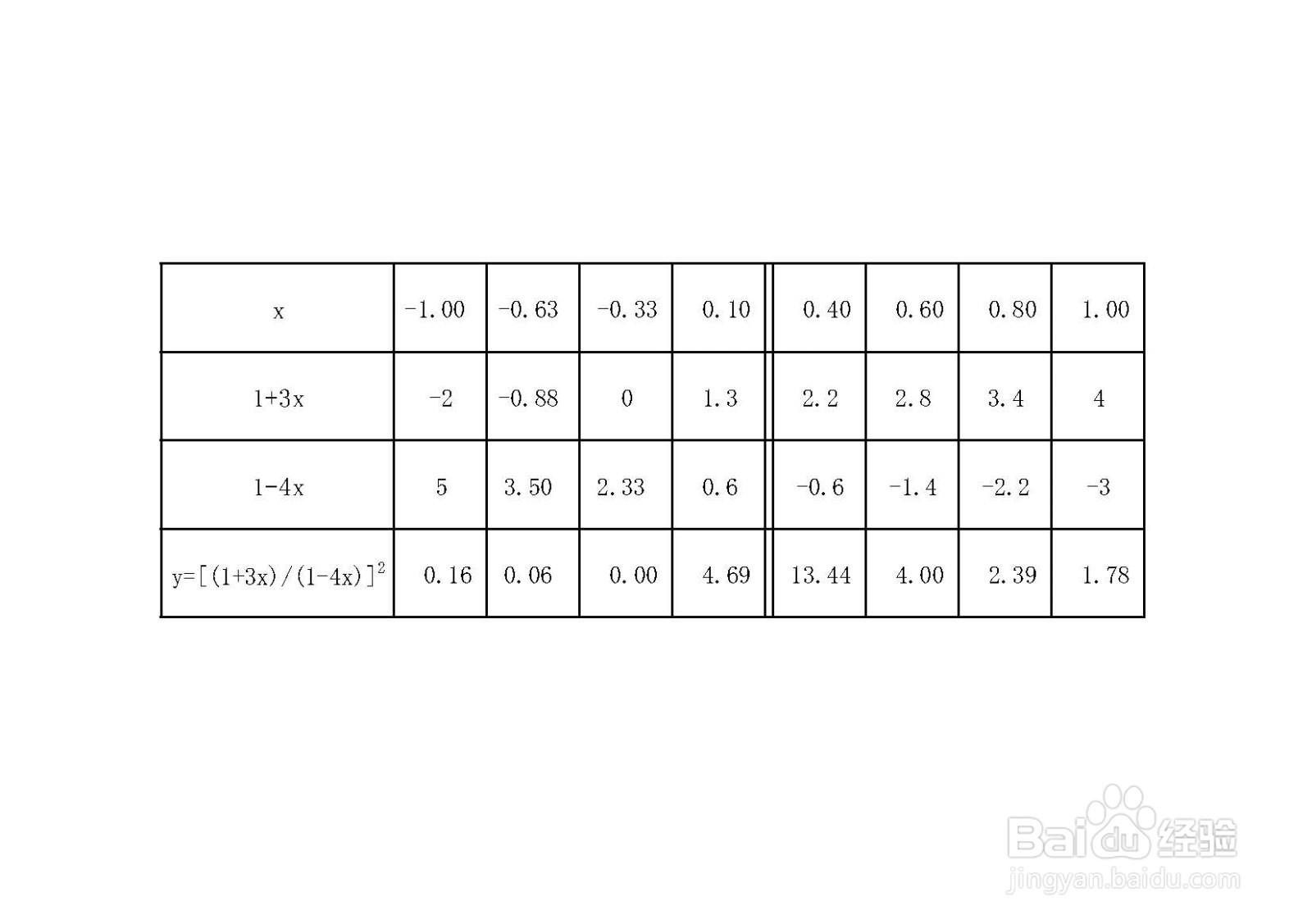
6、函数[(1+3x)/(1-4x)]^2的五点图,函数[(1+3x)/(1-4x)]^2上部分点,解析如下:
7、根据以上函数的定义域、凸凹性、极限、凸凹等性质,通过五点图法,解析函数[(1+3x)/(1-4x)]^2的示意图如下: