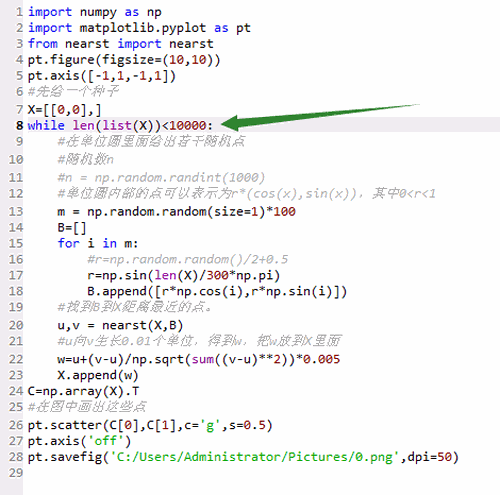
用python3绘制DLA分形图

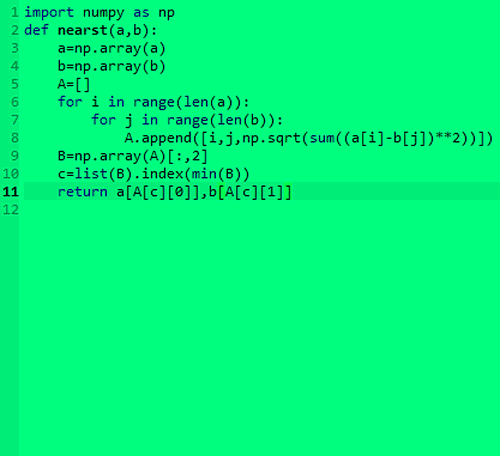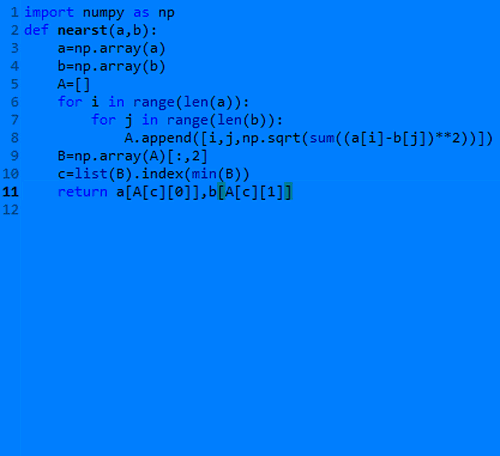
1、构造一个自定义函数，判断平面上两组点集之间距离最近的两个点。import numpy as npdef nearst(a,b): a=np.arra烤恤鹇灭y(a) b=np.array(b) A=[] for i in range(len(a)): for j in range(len(b)): A.append([i,j,np.sqrt(sum((a[i]-b[j])**2))]) B=np.array(A)[:,2] c=list(B).index(min(B)) return a[A[c][0]],b[A[c][1]]把这个代码保存为nearst.py，放到指定文件夹里面。

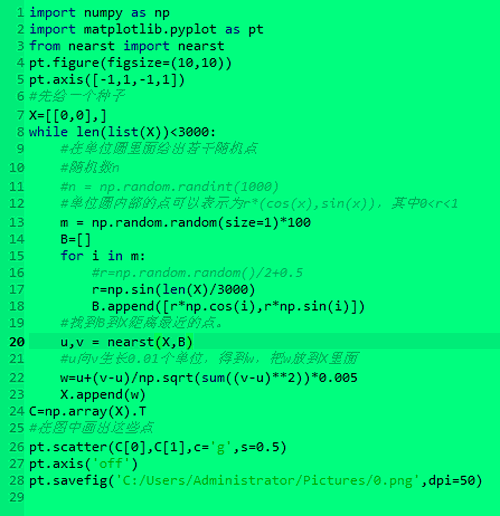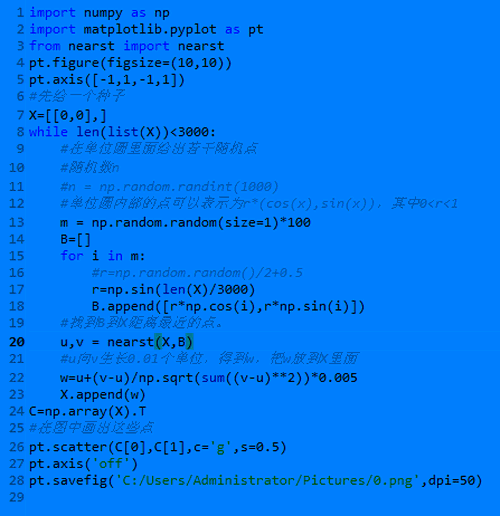
2、在这个指定的文件夹里面，创建一个新的py文件，输入下图的代码。

3、运行之后，得到下面的图形。

4、如果把随机生长的次数定为5000，就得到如下图形。

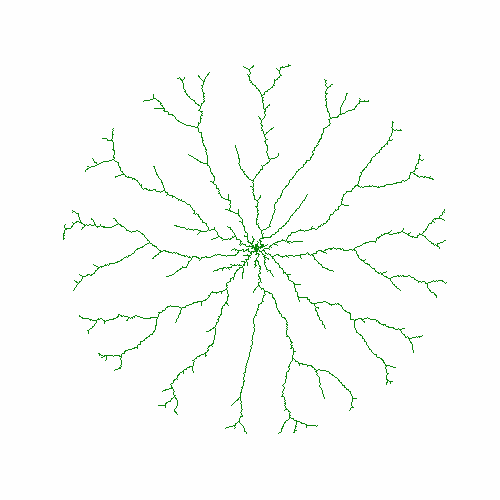
5、如果把代码的r改为：r=np.floor(len(X)/100)/30图形如下。

6、把r改为：r=np.sin(len(X)/3000*np.pi)

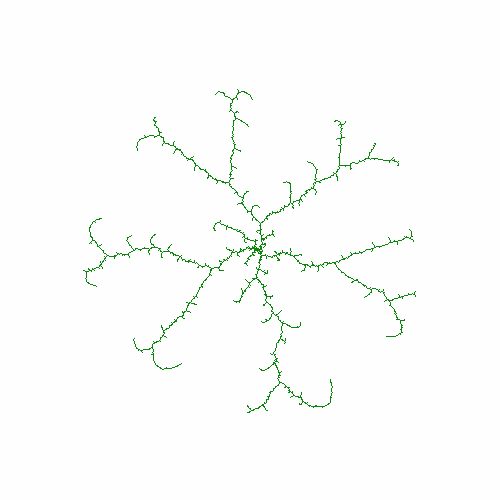
7、r=np.sin(len(X)/300*np.pi)

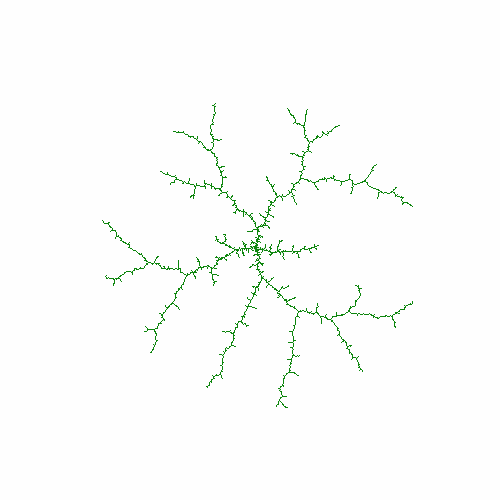
8、最后，画一个生长10000次的DLA模型。