数论：欧拉函数的计算与性质（Mathematica）

1、性质1：当p为素数时，p^n的欧拉函数值，等于(p-1)p^(n-1)。下面，我尺攵跋赈们举例验证。首先使用Prime函数产生10个素数，依次令n等于2,3,4,5,10计算欧拉函数。

3、下边我们举例简要说明原因。p^n的质因子只有p。故与p^n不互素的只有p的倍数，即0,p,2p,3p...p^n-p。

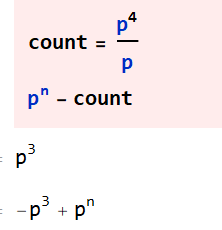
5、性质2：欧拉函数的极性。如图，计算m*n的欧拉函数值，其中m和n互素。则EulerPhi[m*n]=EulerPhi[m]*EulerPhi[n]。如果m和n不互素则不成立。

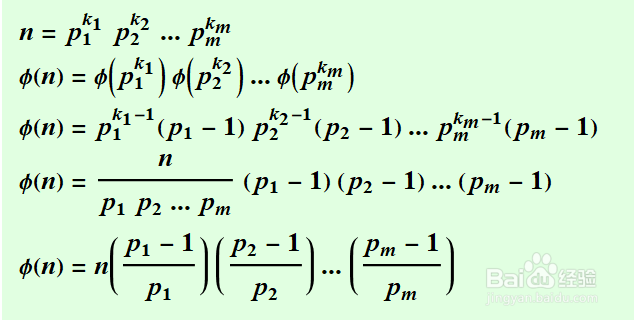
7、如图举了一个实际的例子，计算EulerPhi[738]。把这个数质因子分解，质因子有2,3,41。把这三个数带入最终公式，算得240。