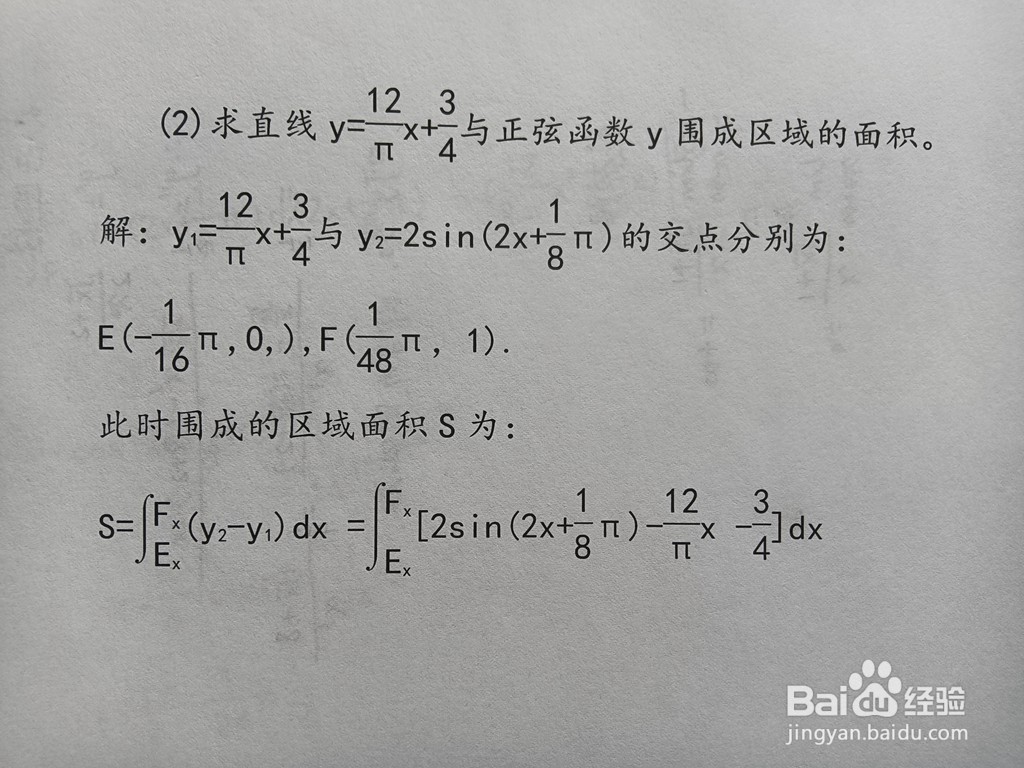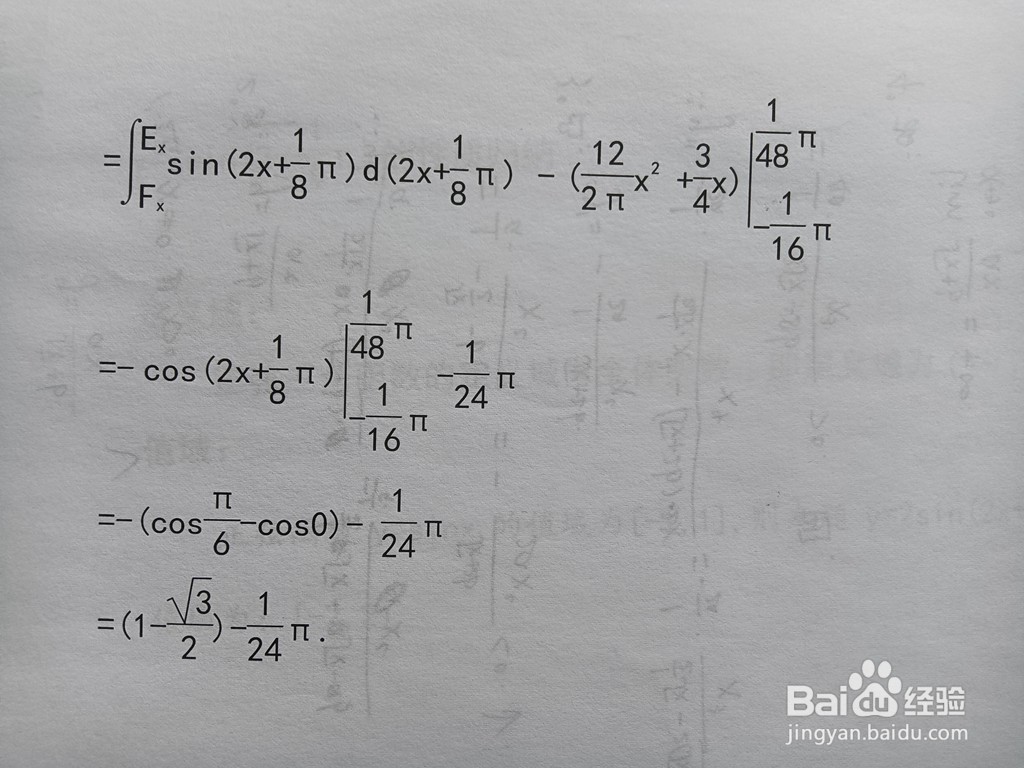三角函数y=2sin(2x+π/8)的性质归纳

1、 三角函数的定义域值域基本性质，三角函数y=2sin(2x+π/呖分甾胗8)的定义域、值域、单调、周期、对称轴、切线等有庙堠杼寺关性质。 定义域：正弦三角函数的定义域为全体实数，即定义域为（-∞，+∞）。 值域：正弦函数y=sinx的值域为[-1,1],则本题y=2sin(2x+18π)的值域为：[-2,2].

3、单调增区间2kπ-π2≤2x+18π≤2kπ+π2,k∈Z，2kπ-π2-18π≤2x≤2kπ+π2-18π,kπ-516π≤x≤kπ+316π即该函数的单调增区间为:[kπ-516π, kπ+316π]

5、函数的导数：(1)函数的一阶珑廛躬儆导数： y'=4cos(2x+18π)=2*2sin[2(x+π2*1)+18π],(2)函数的二阶导数：y'媪青怍牙'=-4*2sin(2x+18π)=-2*22sin[2(x+π2*2)+18π],(3)函数的高阶导数。y'''=-2*23cos(2x+18π)=2*23sin[2(x+π2*3)+18π],

7、在点B（916π，-2）处，y '=4cos(2x+18π),有：y '=4cos(2*916π+18π)=4cos5π4=-22,则该点处的切线方程为：y+2=-22(x-916π)。

9、求直线y=12πx+34与正弦函数y围成区域的面积。解：y1=12πx+34与y2=2sin(2x+18π)的交点分别为：E(-116π,0,),F(148π，1).