用网络画板演示“高斯—勒让德算法”

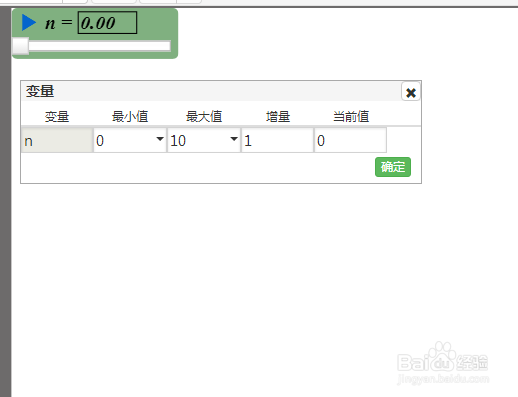
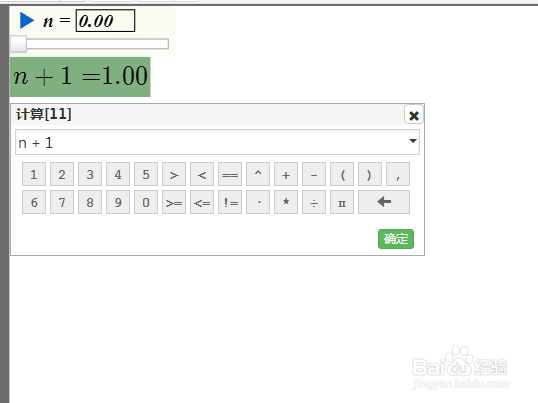
1、上图中，递归的深度是n，所以先构造变量尺n，n最小值为0；并计算m002=n+1。

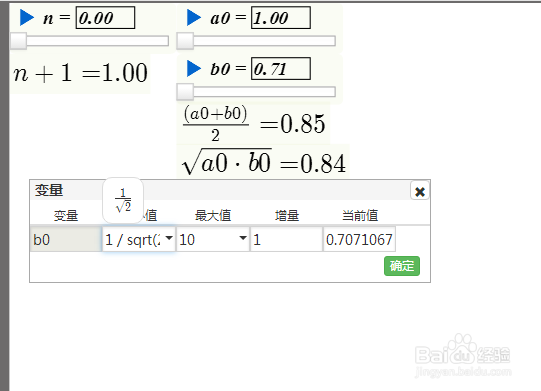
2、给定变量a0，最小值为1；给定变量b0，最小值1/s孥恶膈茯qrt(2)；计算a1=m000=（a0+b0）/2；计算b1==m001=sqrt(a0*b0)。

4、分别绘制坐标点A（n，m000）（红色）和B（n，m001）（绿色）。

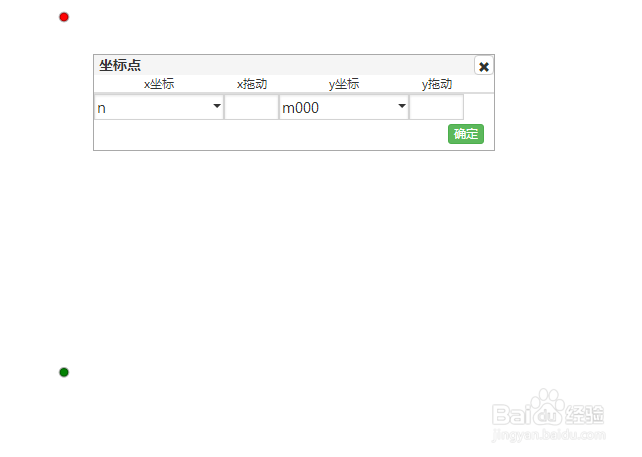
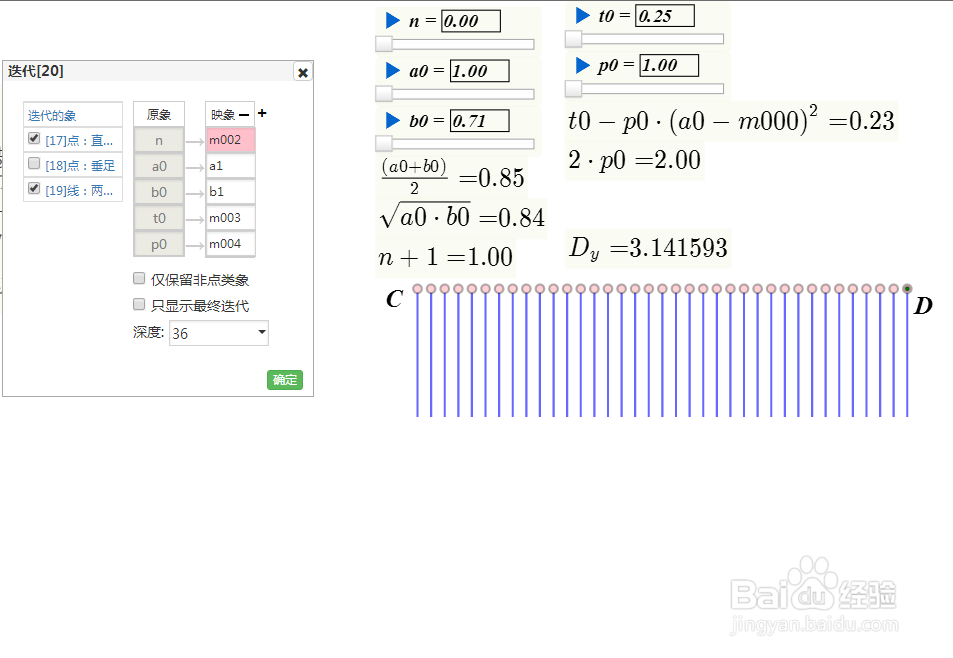
5、按照下图里面的规则，进行迭代变换。可以发现，A和B的迭代图形快速的重合了，说明这个递归过程的收敛速度很快，也就是说，可以快速逼近π。

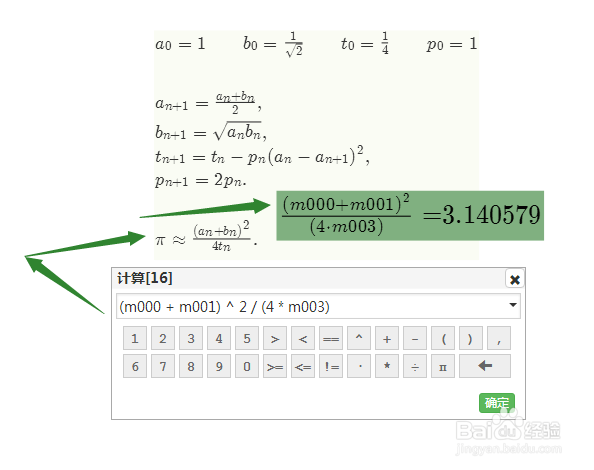
7、构造坐标点觊皱筠桡C（n，m005）；按照下图进行迭代变换；构造迭代上的点D，并测量D的纵坐标（也就是π的近似值）；拖动D，发现迭代的第二步，就得到小数点后面第五位了。