线性代数：矩阵相似和对角化

授人予鱼不如授人予渔，在《线性代数》的学习中，方法尤为重要。下面就让我们一起解决《线性代数》中令人头痛的——矩阵相似和对角化问题吧！如果您对——矩阵相似和对角化的学习比较吃力，建议您先学习——舄踣焱莠伴随矩阵和逆矩阵，传送门开启，嘛咪嘛咪哄！

工具/原料

线性代数课本

笔、纸

一、矩阵相似的定义和性质

1、矩阵相似定义，如下：

3、相似矩阵有相同的特征向量和特征值：

5、矩阵相似和对角化的注意点：

2、题目一，解答如下：

四、对角化和特征值例题

1、例题1、由特征值、特征向量求矩阵：

五、实对称矩阵的含义

1、一定可以对角化的矩阵称为实对称矩阵：

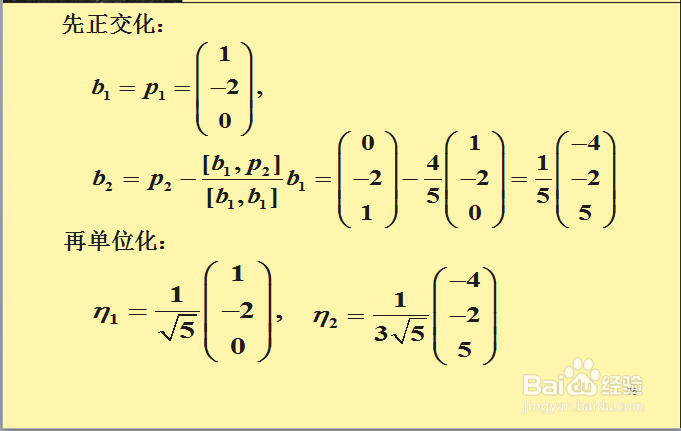
七、结语

1、关于矩阵相似和对角化已经讲解完了，祝贺您今天又学习了新知识。