二次函数交点式怎么用
1、二次函数的一般式是:y=p*x^2+q*x+r,开口不是向上,就是向下。
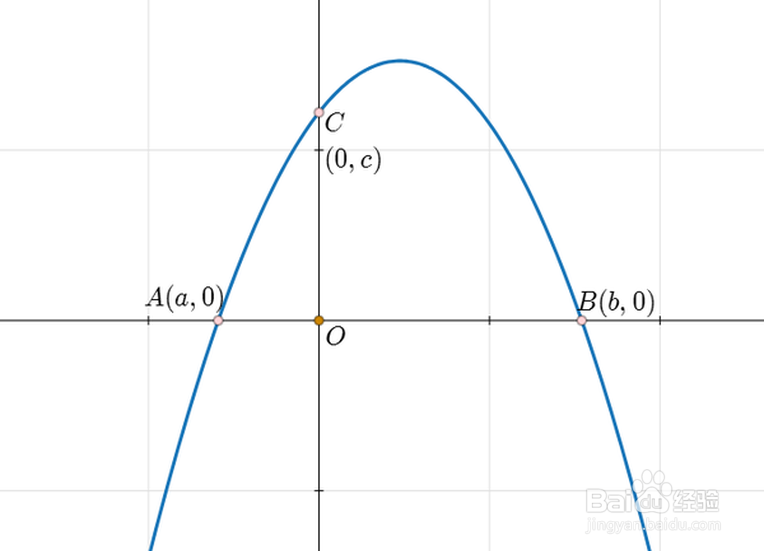
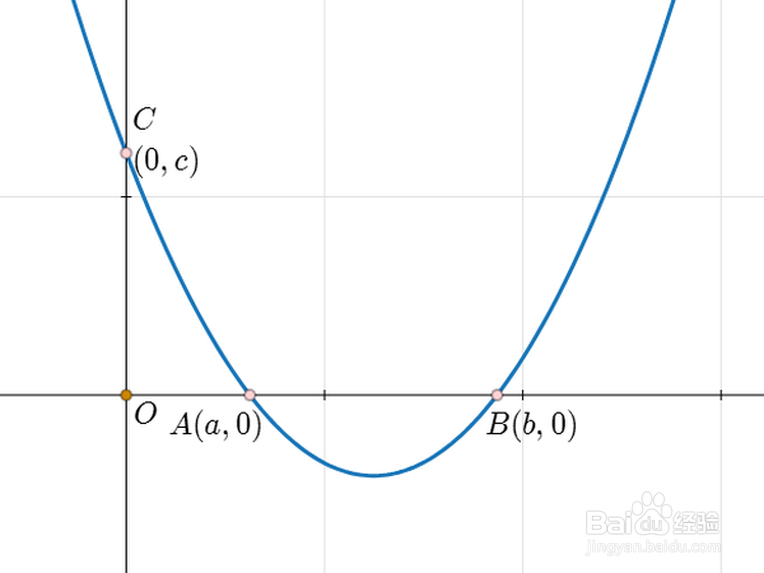
2、二次函数与x轴的交点A和B的坐标分别是:A=(a,0)、B=(b,0),那么,可以得出二次函数的一种因式分解形式:y=k*(x-a)*(x-b),无论x等于a,还是等于b,y都等于0。
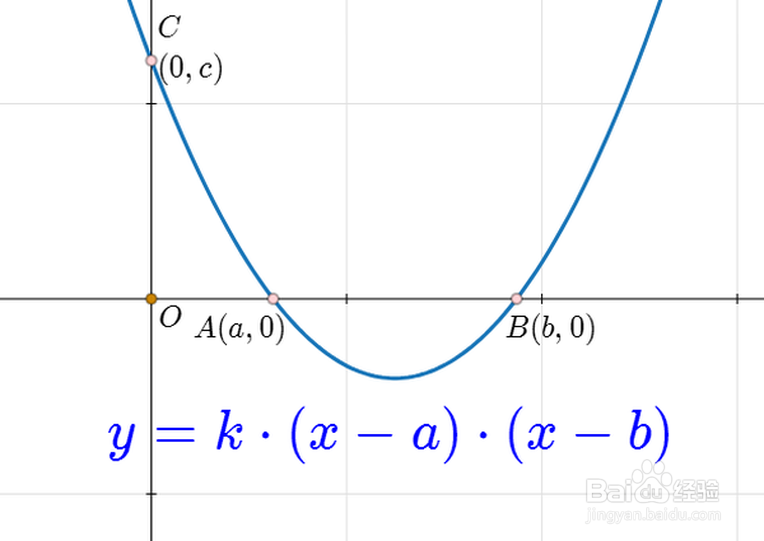
3、二次函数与y轴的交点坐标是:C=(0,c),当x=0的时候,y=c,代入到上式,可以得出系数k的值。
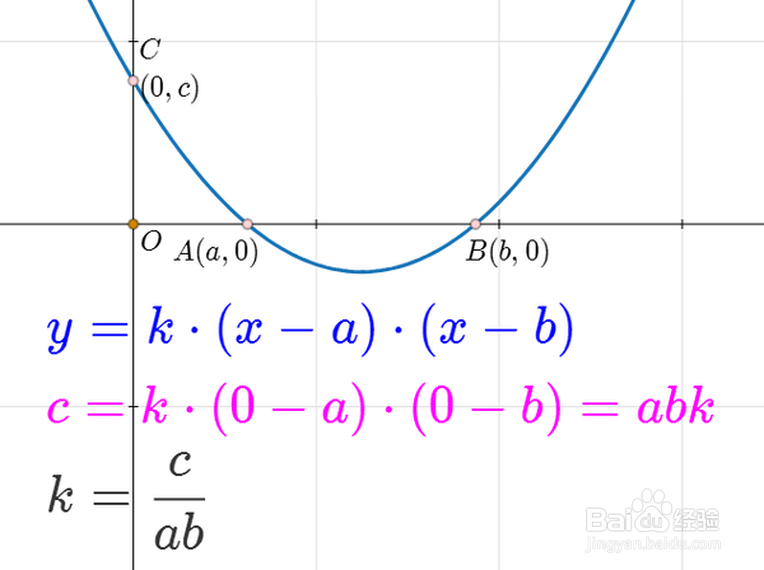
4、于是,我们得到了二次函数的交点式方程:y=(c/ab)*(x-a)*(x-b)。
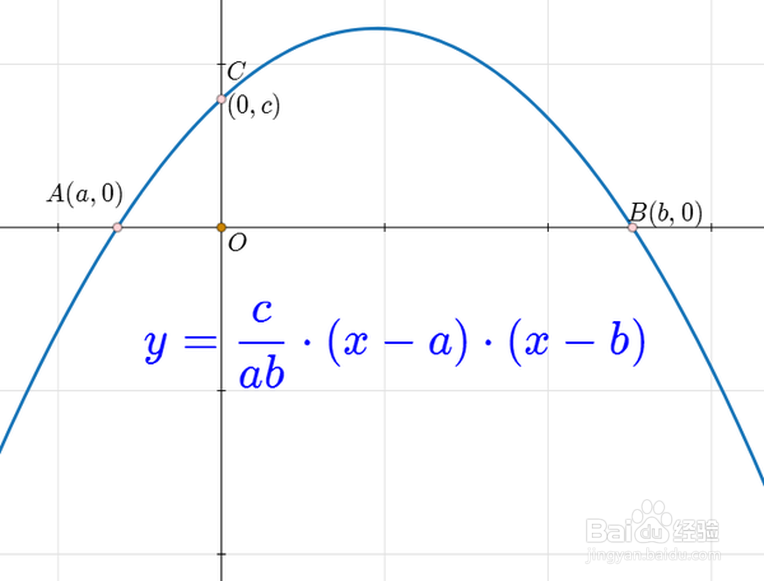
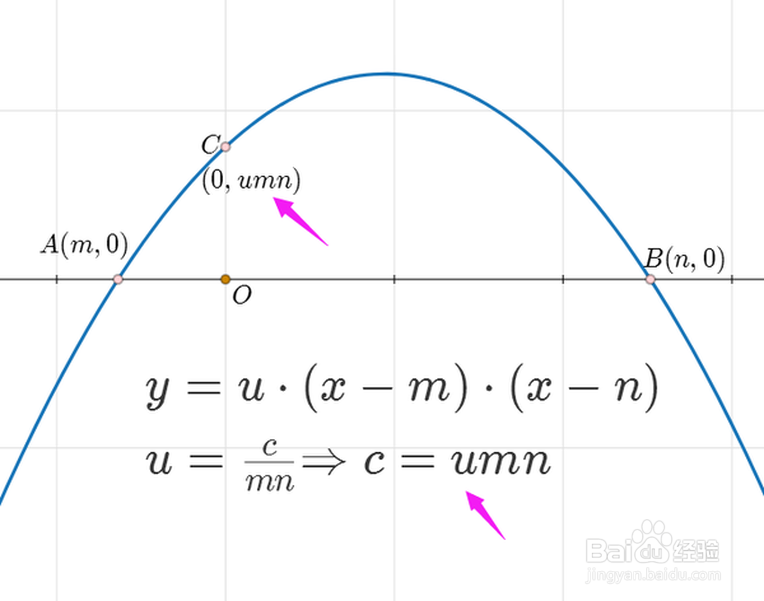
5、通过二次曲线的交点式,可以快速求出这个二次函数与坐标轴的交点坐标。比如,二次函数y=u*(x-m)*(x-n),且m<n,那么它与x轴的交点坐标就是:A=(m,0)、B=(n,0),A在B的左侧。
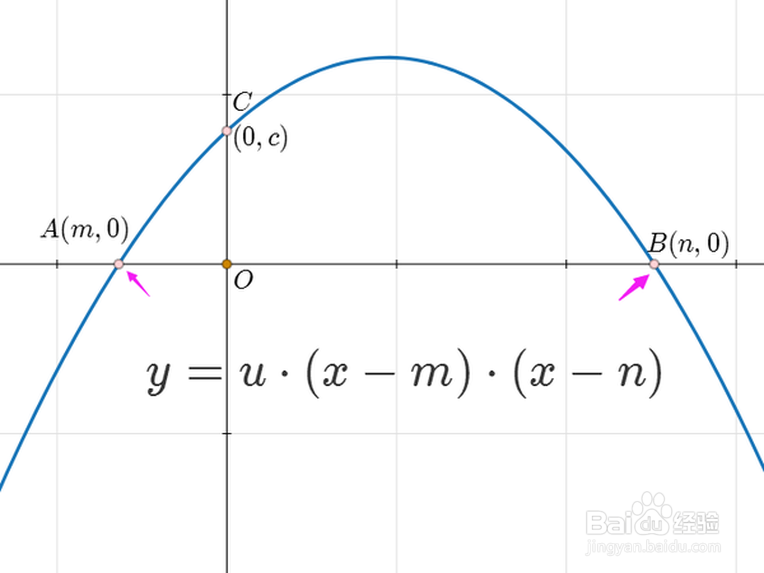
6、关键是与y轴的交点坐标:C=(0,c)。因为u=c/(mn),所以c=umn。