【抽象代数】正四面体群的三维矩阵表示
1、正四面体群最直接的表示,就是群元素作用于正四面体。
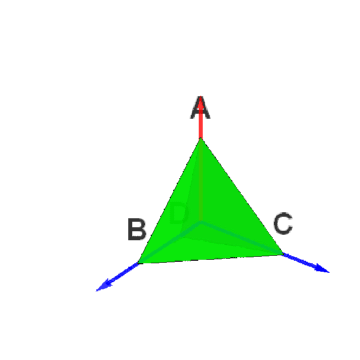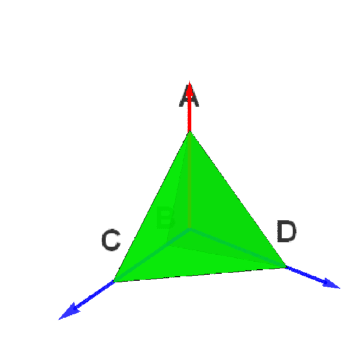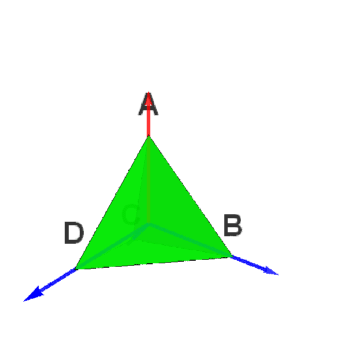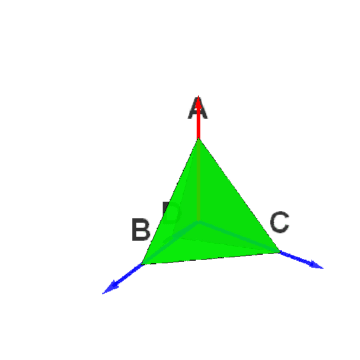
2、如果O为正四面体的中心,选择向量集合{蚪嬷吃败OB、OC、OD}作为三维空间的基,那么,点B的坐标就可以写为:{1,0,0},点C的坐标就可以写为:{0,1,0},点D的坐标就可以写为:{0,0,1}。进而,点A的坐标可以写为{-1,-1,-1},这是因为O=(A+B+C+D)/4。
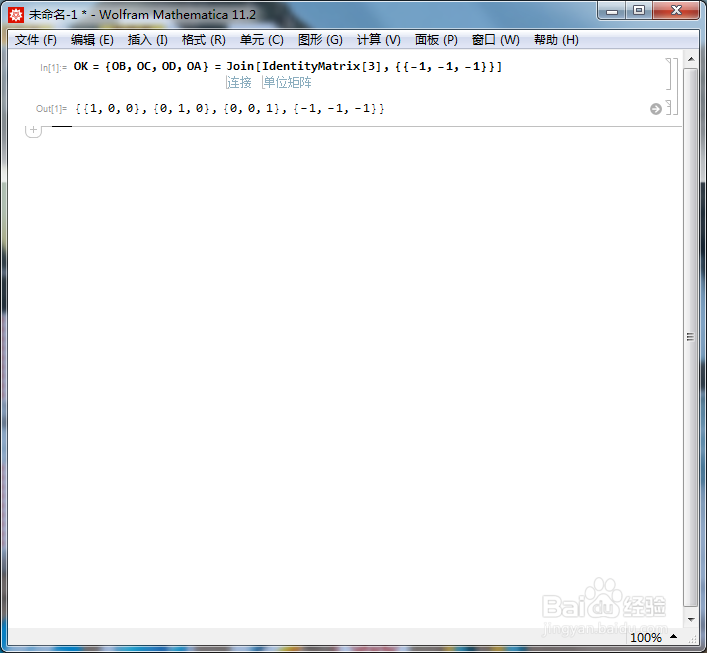
3、以OA为旋转轴,旋转120°,这个变换记为a,它把{OB,OC,OD}变成了{OC,OD,OB}。因此,a对应的旋转矩阵可以表示为:
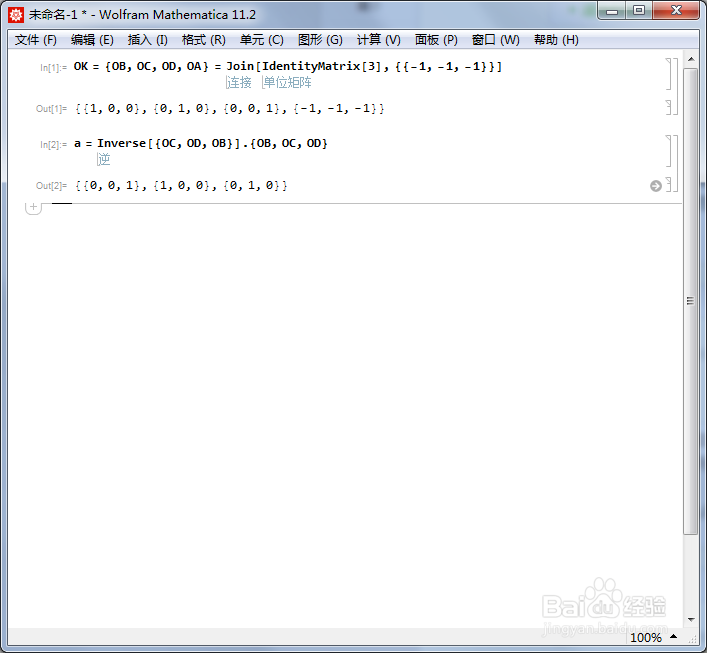
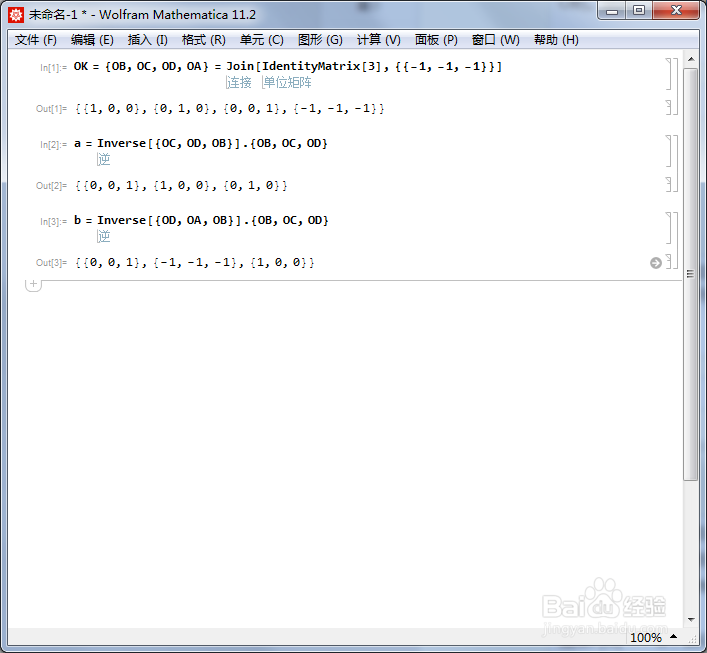
4、设AC的中点为X,BD的中点为Y,以XY为旋转轴旋转180°,把这个变换记为b,它把{OB,OC,OD}变成了{OD,OA,OB}。因此,b对应的旋转矩阵可以表示为:
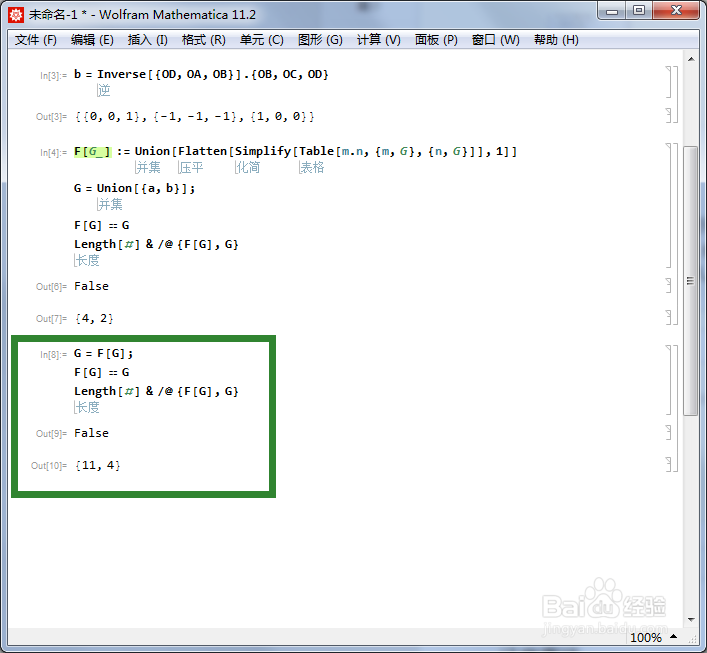
5、这样,a和b就可以生成整个正四面体群。先用集合{a,b}作乘法表,并查看乘法表里面的元素是否能够成为一个群:F[G_] := Union[Flatten[Simplify[Table[m.n, {m, G}, {n, G}]], 1]]G = Union[{a, b}];如果F[G] == G,则G为群。但是此时,F[G]四个元素,而G有两个元素,因此G不是群。
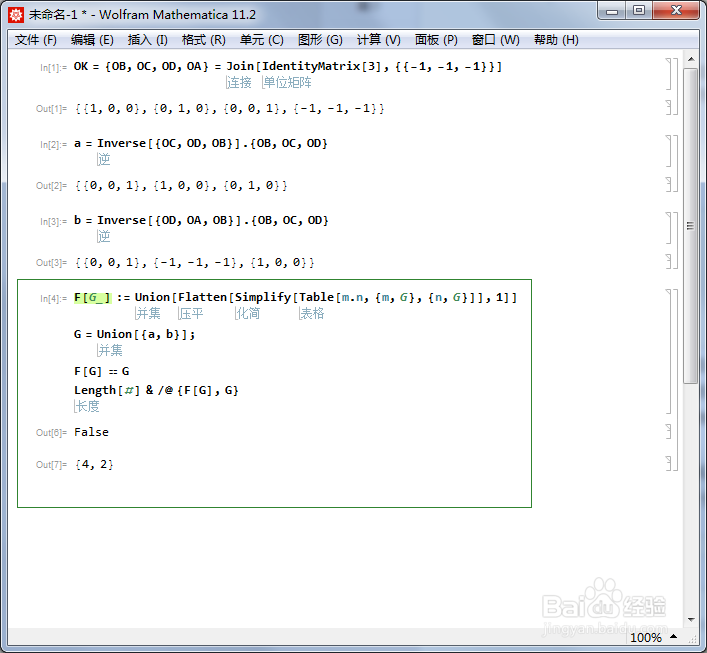
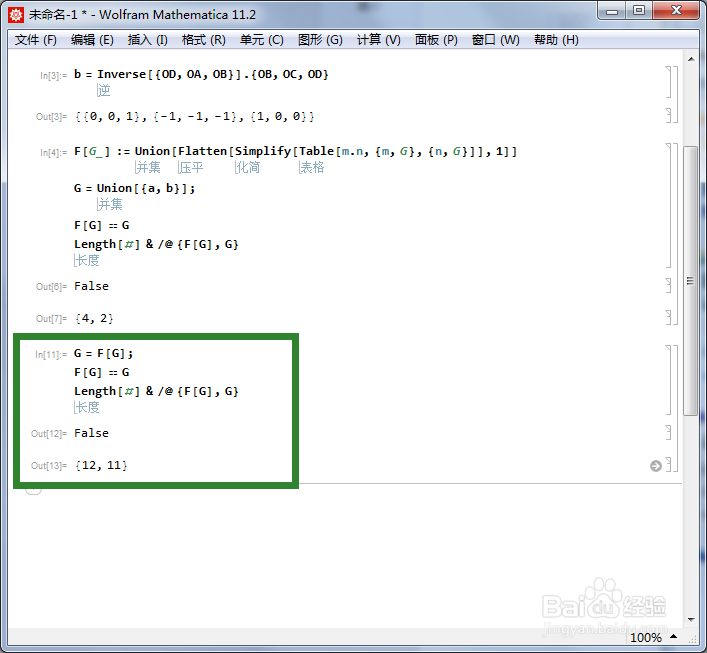
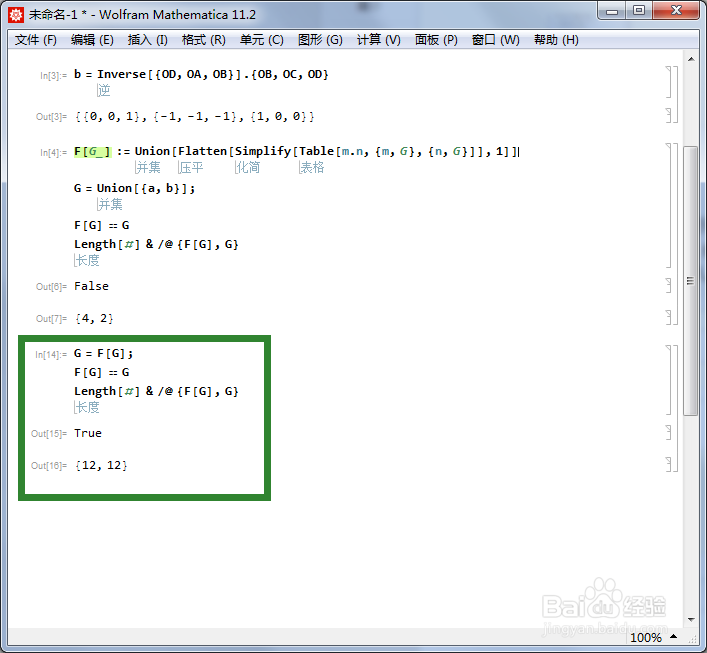
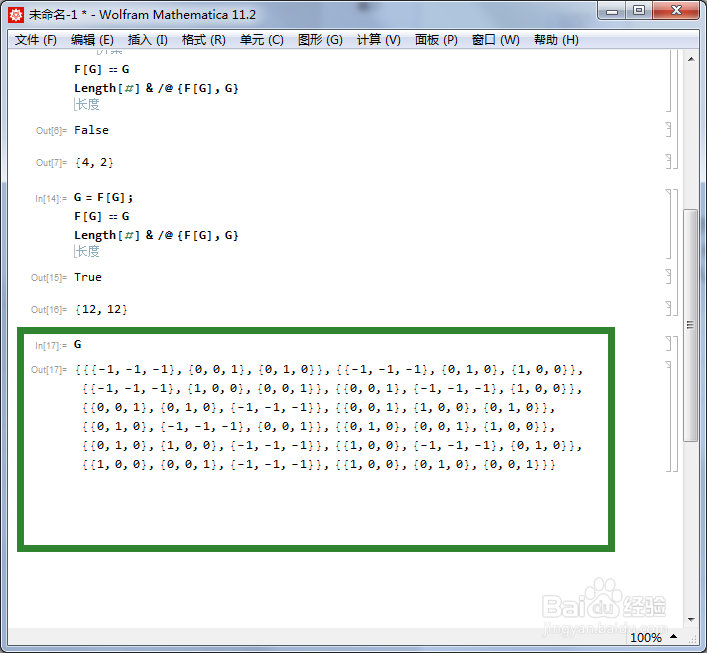
6、用F[G]代替G。G = F[G];F[G] == GLength[#] & /@ {F[G], G}这个程序运行三次,终于得到F[G] == G,此时G有12个元素。这恰好是正四面体群的一个三维表示。