函数y=3x^5+x+3的图像如何画
1、 函数y=3x^5+x+3为幂函数的四则运算,可知函数的自变量可以取全体实数,即定义域可以为:(-∞,+∞)。

2、 函数的单调性也叫函数的增减性。当函数 f(x) 的自变量在其定义区间内增大(或减小)时,函数值f(x)也随着增大(或减小),则称该函数为在该区间上具有单调性。 本题函数y=3x^5+x+3的单调性,求出函数的一阶导数,通过函数的一阶导数,判断函数的单调性,进而求出函数的单调区间。y‘=3*5x^4+1=15x^4+1,可知,函数在定义域上为增函数。

3、 举例求解点A(-1,-1)处的切线,主要步骤如下:此时y'=15+1=16,由直线的点斜式可求出点A处的切线方程为:y+1=16(x+1).
4、 函数y=3x^5+x+3的凸凹性,通过函数的二阶导数,解析函数的凸凹性。

5、 如果函数f(x)在区间I上二阶可导,则f(x)在区间I上是凹函数的充要条件是f''(x)>=0;f(x)在区间I上是凸函数的充要条件是f''(x)<=0。
6、 由函数y=3x^5+x+3性质,解析函数的极限,判断函数在无穷大处的极限。函数在无穷大处的极限为无穷大大,在x=0处时,y=3。

7、 函数y=3x^5+x+3五点图,由函数表达式,解析函数部分点如下:例如x=0时,y=3;x=1时,y=3*1+1+3=7;x=-1时,y=-3*1-1+3=-1.
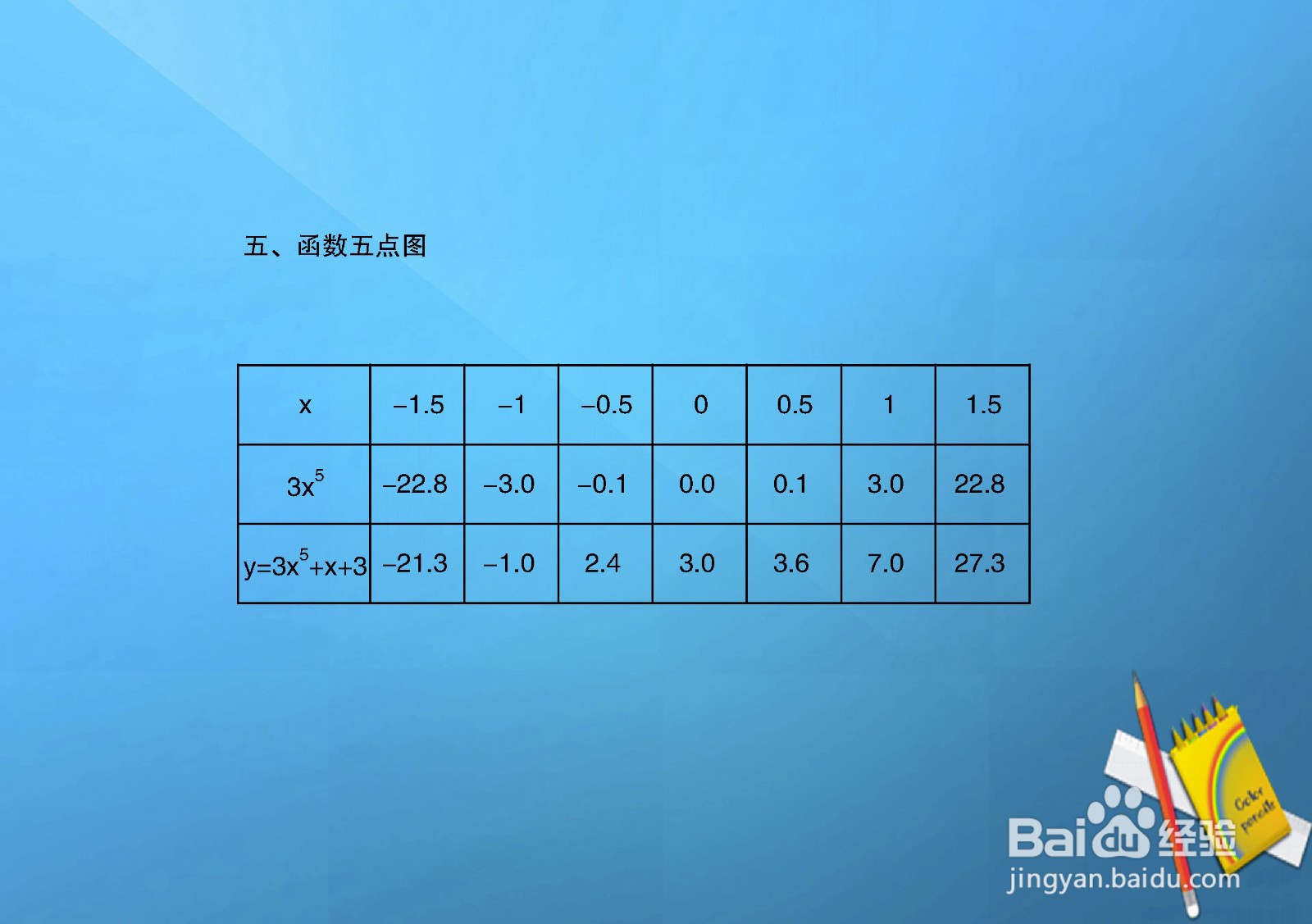
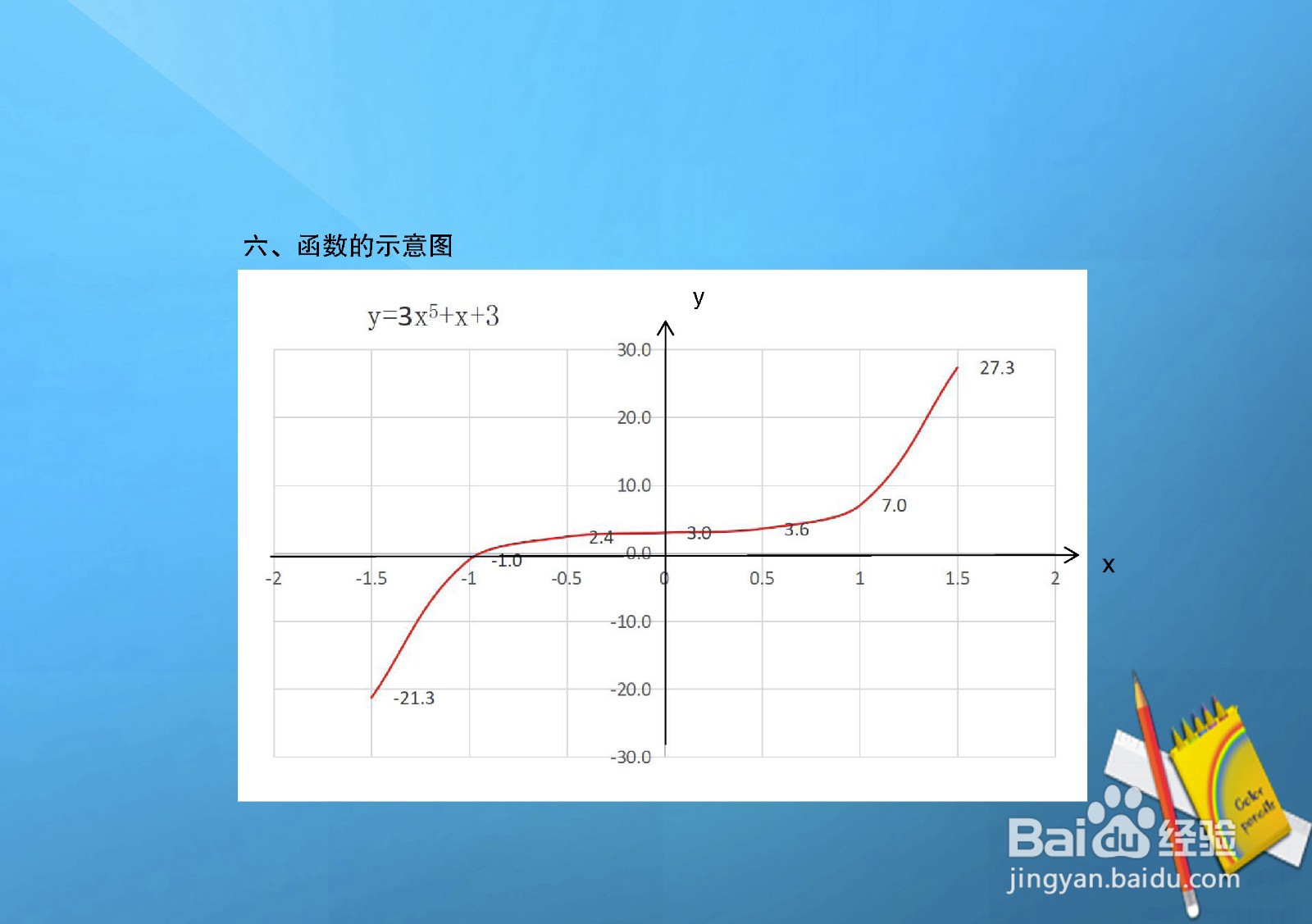
8、 根据函数y=3x^5+x+3的定义域、值域、极限等性质,并通过函数的导数判断函数的单调性、凸凹性,综合解析函数的示意图如下:
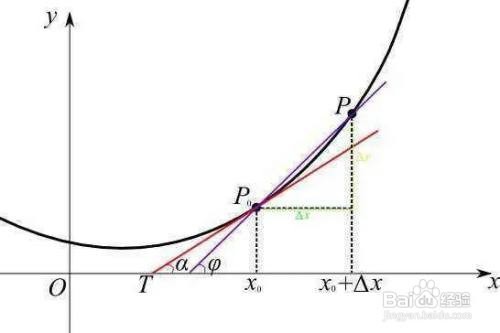
9、 导数,是微积分中的重要基础概念。当自变量的增量趋于零时,因筐毙险裆变量的增量与自变量的增量之商的极限。一个函数存在导数时,称这个函数可导或者可微分。可导的函数一定连续。不连续的函数一定不可导。导数实质上就是一个求极限的过程,导数的四则运算法则来源于极限的四则运算法则。
10、 若函数y=f(u)的定义域是B,u=g(x)的定义域是A,则翱务校肢复合函数y=f[g(x)]的定义域是D={x|x∈A,且g(x)∈B} 综合考虑各部分的x的取值范围,取他们的交集。复合函剞麽苍足数的单调性具有规律,即"增+增=增;减+减=增;增+减=减;减+增=减",可以简化为"同增异减"。
