怎么用抽象代数的思想,解同余方程组
本文,用抽象代数的方法,来求解下面的同余方程组:3 x+4 y+5 z≡2 (mod 17)6 x+y≡5 (mod 17)2 x+10 y-z≡13 (mod 17)

工具/原料
电脑
Mathematica
初解
1、首先,这个方程组可以用矩阵的的乘法来表示:A.X==B
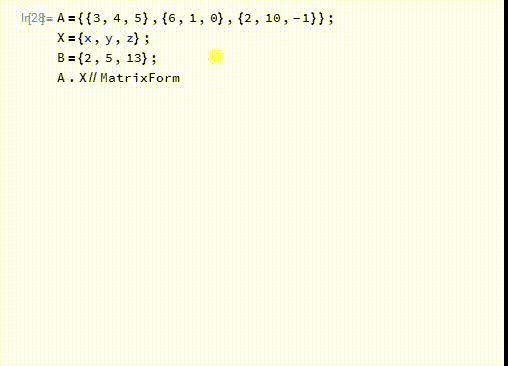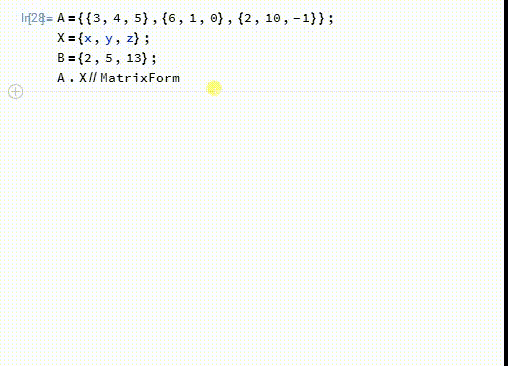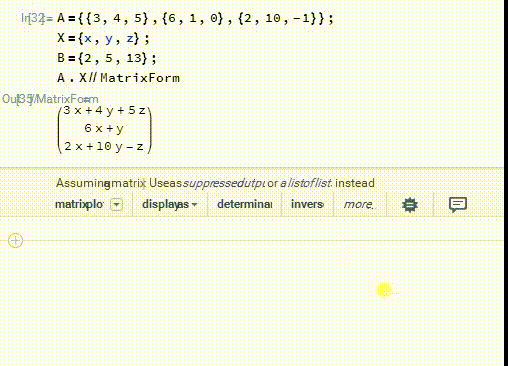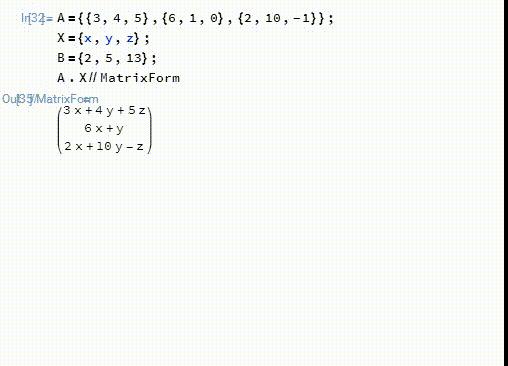
2、模17的剩余类组成一个域——F17:在这个域里面,A的逆矩阵是:A2={{16,3,12},{6,4,13},{7,12,13}}

3、那么,X就可以用矩阵乘法表示出来:X=A2.B那么答案就是X={x,y,z}={-1,-3,5}(mod 17)

检验
1、注意,上面的答案不知道出什么问题了,跟另一个方法得到的答案不一样,所以,检验答案,是必不可少的步骤。Mathematica可以直接在F17里面计算A的逆——A3,见下图。
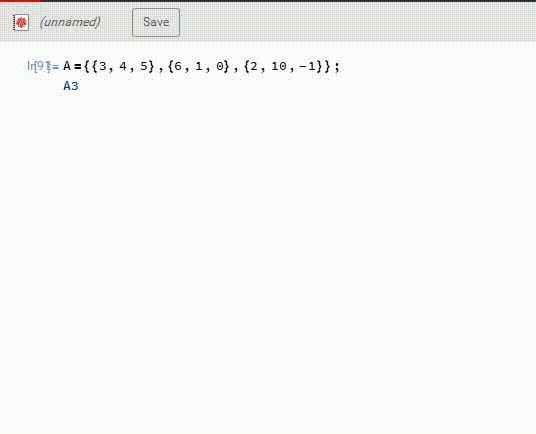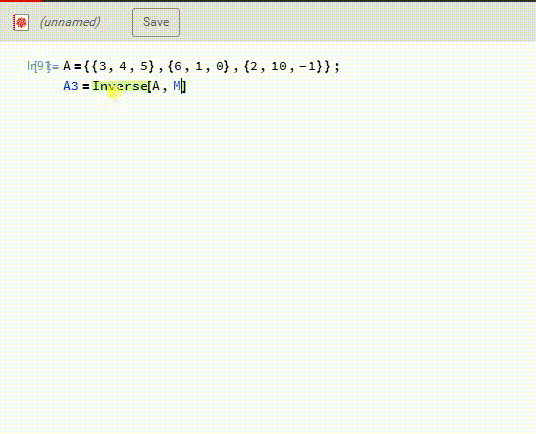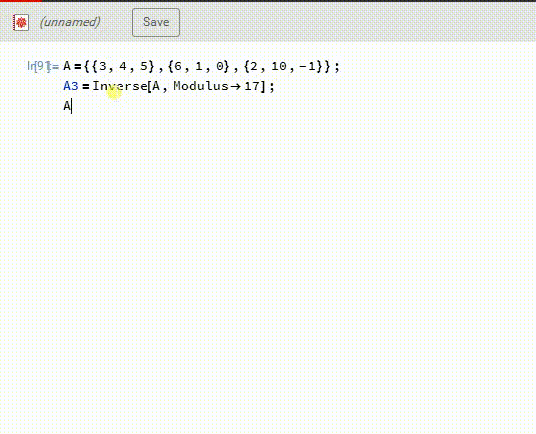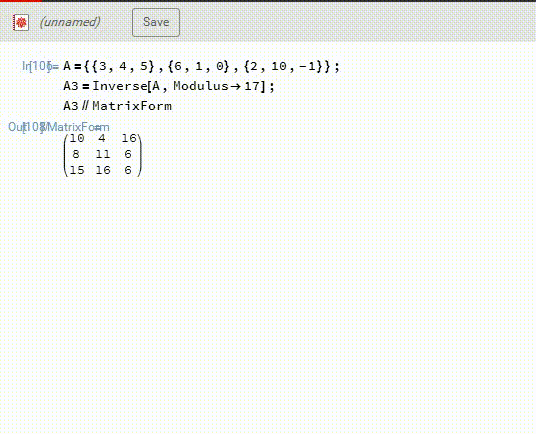
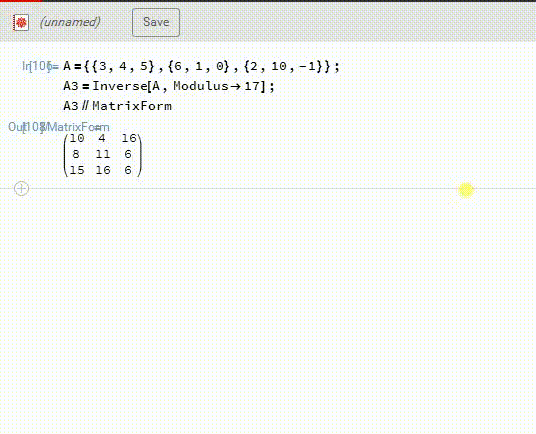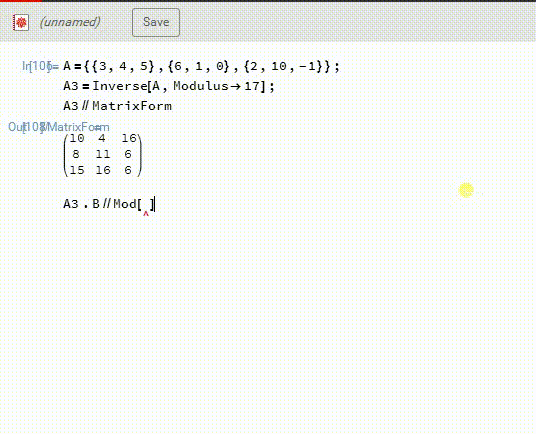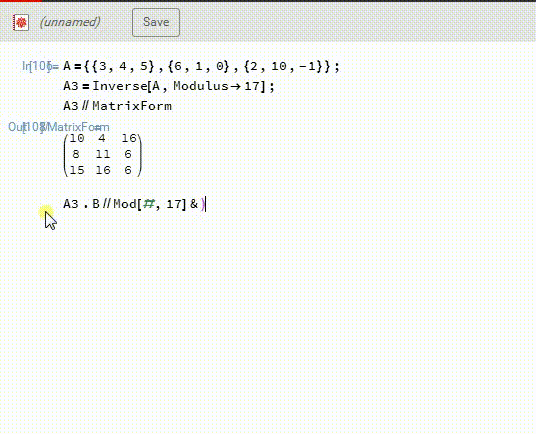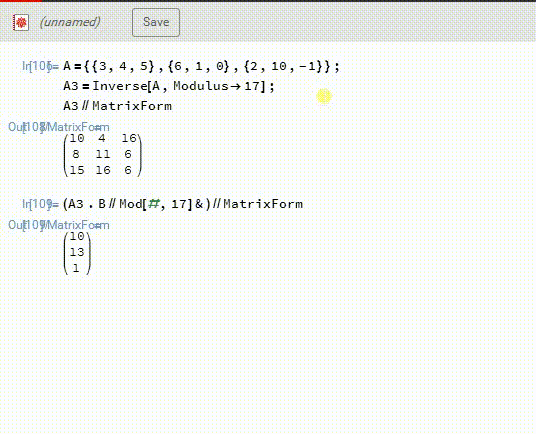
2、然后,A3.B,再模17,得到X。这一次得到的答案是X={10,13,1},和上面的答案不相同。
再检验
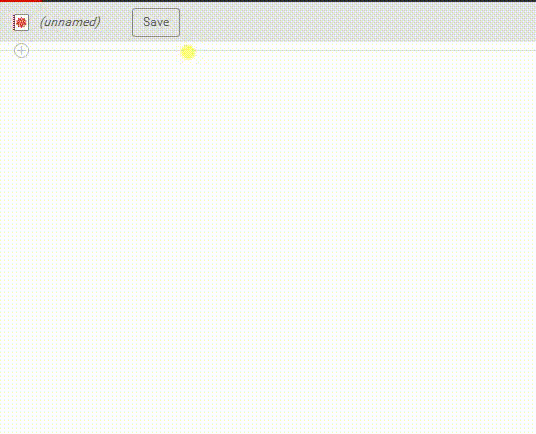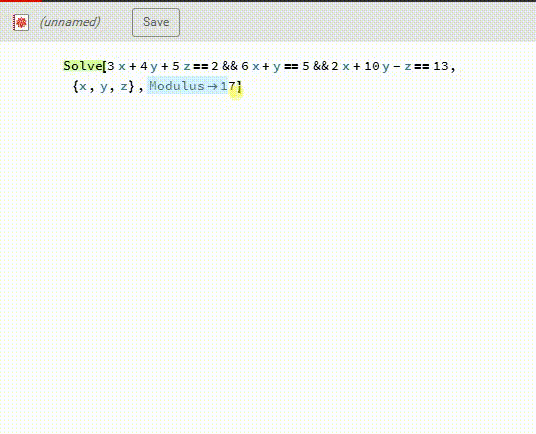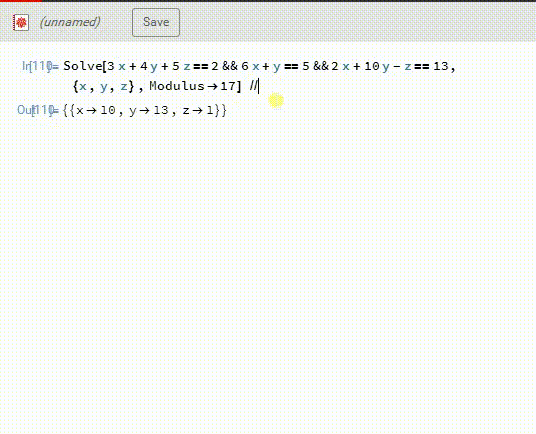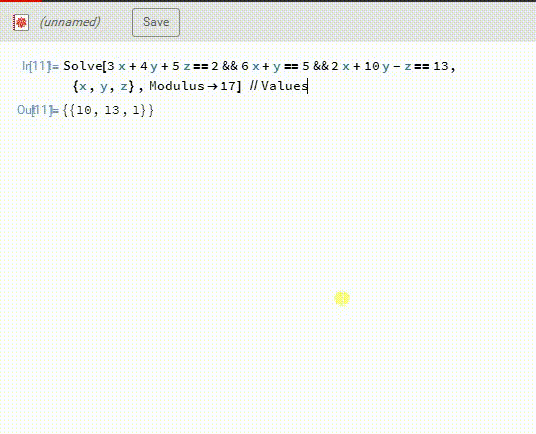
1、如果两个方法得的结果不同,就需要再检验,这一次,直接用Mathematica解同余方程组:Solve[……,{x,y,z},Modulus->17]得到的答案也是X={10,13,1}。