用Mathematica处理简单的微积分方程
我们来学习一下用Mathematica解决简单的微积分的具体方法。
工具/原料
电脑
Mathematica
微分和积分
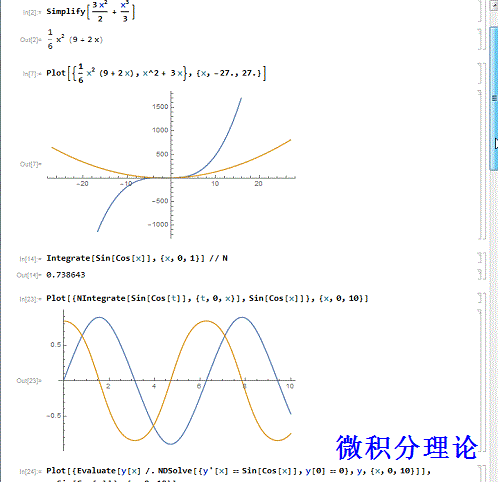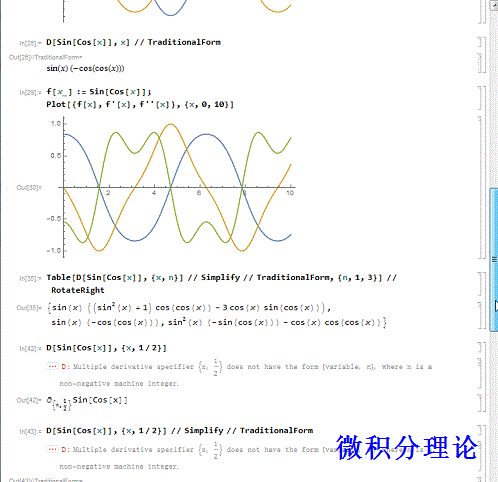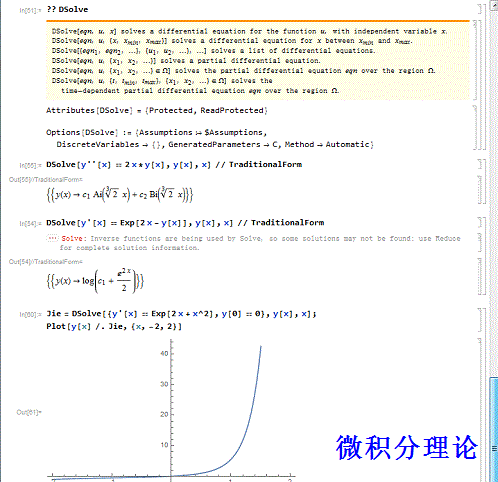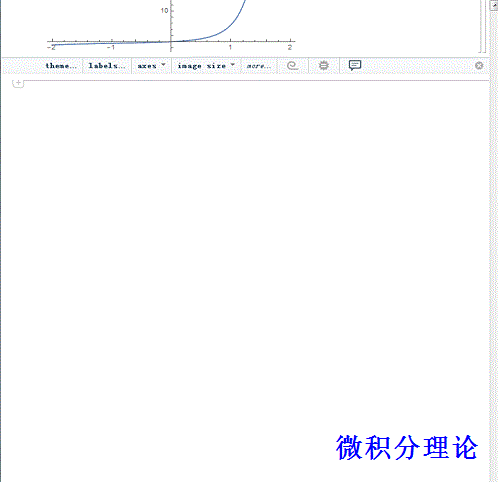
1、用Mathematica求函数的不定积分。用到的函数是Integrate,格式是Integrate[关于x的函数, x],比如求函数x^2 + 3 x的原函数:Integrate[x^2 + 3 x, x]并对结果加以化简,把函数及其原函数画到一起,加以比较:Simplify[Integrate[x^2 + 3 x, x]]Plot[{1/6 x^2 (9 + 2 x), x^2 + 3 x}, {x, -27., 27.}]注意,Mathematica忽略了不定积分后面的常数。
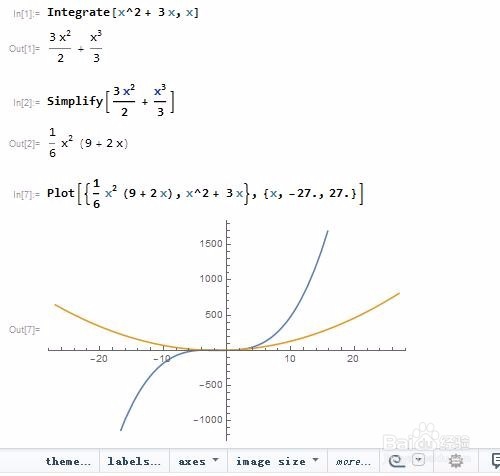
2、用Mathematica求定积分。有些函数是不能求出不定积分的,但是可以求出定积分,如sin(cosx)的原函数:Integrate[Sin[Cos[x]], x]但可以尝试着求它的定积分:Integrate[Sin[Cos[x]], {x, 0, 1}] // N或者NIntegrate[Sin[Cos[x]], {x, 0, 1}]这里当然是给出数值解,而不是精确值!想要获得更多细节,可以先输入两个等号,然后输入相应代码!
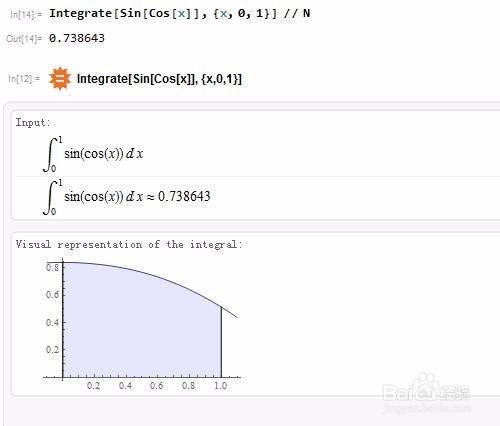

3、就算不能求出原函数,仍旧可以作出原函数的图像(暂时忽略后面的常数):Plot[{NIntegrate[Sin[Cos[t]], {t, 0, x}], Sin[Cos[x]]}, {x, 0, 10}]或Plot[{Evaluate[ y[x] /. NDSolve[{y'[x] == Sin[Cos[x]], y[0] == 0}, y, {x, 0, 10}]], Sin[Cos[x]]}, {x, 0, 10}]感谢Mathematica智囊团的B-天文-frokaikan(541240857)和B-力学-无影东瓜(584281084)的无私帮助!

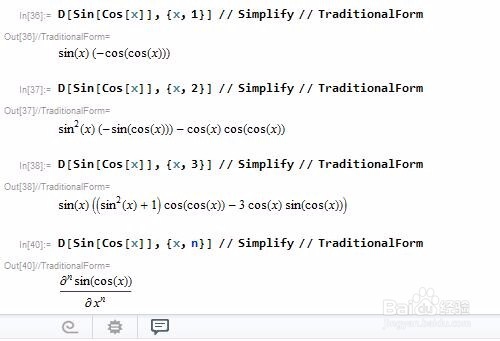
4、用Mathematica求函数的导数。直接用函数D,格式是D[函数f, x],以Sin[Cos[x]]的求导为例:D[Sin[Cos[x]], x] // TraditionalFormTraditionalForm——传统形式,这样看着顺眼!顺便把这个函数的图像、导函数图像、二阶导函数图像绘制在一起:f[x_] := Sin[Cos[x]];Plot[{f[x], f'[x], f''[x]}, {x, 0, 10}]
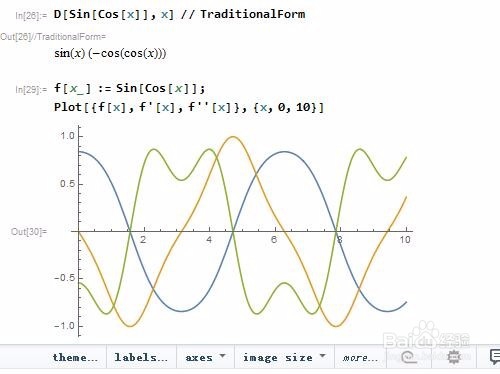
5、求函数的高阶导数。D[Sin[Cos[x]], {x, n}],求函数Sin[Cos[x]]关于x的n阶导数:D[Sin[Cos[x]], {x, 1}] // Simplify // TraditionalFormD[Sin[Cos[x]], {x, 2}] // Simplify // TraditionalFormD[Sin[Cos[x]], {x, 3}] // Simplify // TraditionalFormD[Sin[Cos[x]], {x, n}] // Simplify // TraditionalForm
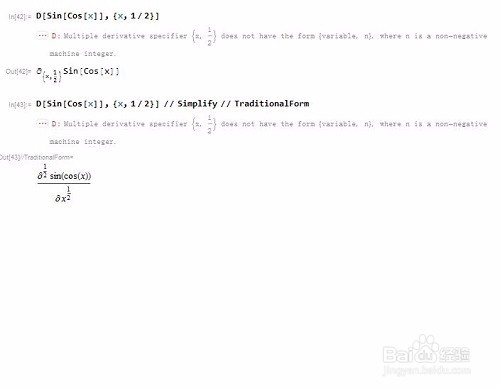
6、函数导数的阶数只能是正整数!D[Sin[Cos[x]], {x, 1/2}]D[Sin[Cos[x]], {x, 1/2}] // Simplify // TraditionalForm这些,都是不允许的!
简单的微分方程
1、首先说明,Mathematica10.0以前的版本不能够使用DSloveValue,但是可以用DSlove,格式是:格式是DSlove[微分方程,函数,自变量]。具体的用法,可以:?DSolve或者?? DSolve

2、举个例子:DSolve[y''[x] == 2 x*y[x], y[x], x] // TraditionalFormDSolve[y'[x] == Exp[2 x - y[x]], y[x], x] // TraditionalForm 第二个代码,会出现提示:Inverse functions are being used by Solve, so some solutions may not be found; use Reduce for complete solution information.

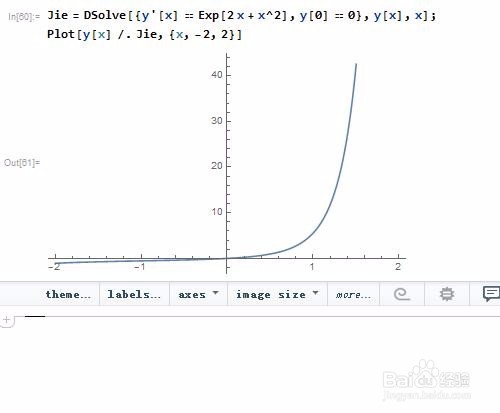
3、可以作出微分方程解的图像。Jie = DSolve[{y'[x] == Exp[2 x + x^2], y[0] == 0}, y[x], x];Plot[y[x] /. Jie, {x, -2, 2}]