画函数y=e^(x+4y)的图像的主要步骤

1、令F＇(y)=0，则y=1/4.当0<y<1/4时，F＇(y)>0;当y>1/4时，F＇(y)<0.所以，当y=1/4时，F(y)有最大值，即：x=F(y)≤F(y)max=-(1+ln4)x≤-(1+ln4)/1≈-2.39即曲线方程的定义域为：(-∞，-2.39]。

3、函数y=e^(x+4y)的单调性，通过函数的一阶导数，求出函数y的单调区间。

5、 函数的凸凹性性，计算该隐函数的二阶导数，通过函数的二阶导数的符号，判断函数的凸凹性，并求解y=e^(x+4y)的凸凹区间。

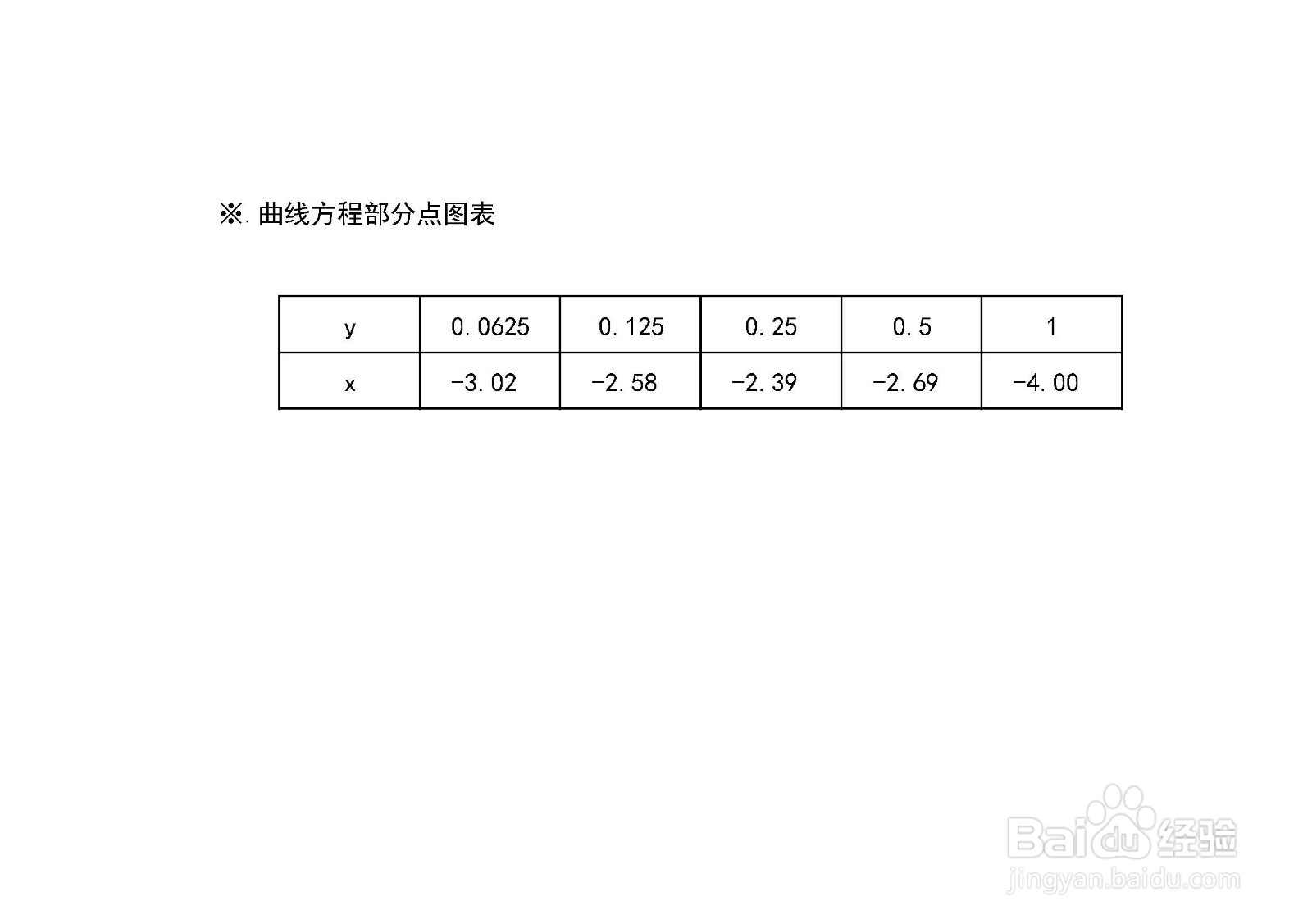
7、函数y=e^(x+4y)上的部分点，函数五点图表如下：